Anyone who has asked this question before and tries to find a solution freehand, so to speak, without help from the literature, without google, Wikipedia or the like, may consider very different possibilities.

Would you e.g. know the exact volume of the earth, plus your average density, could you give the weight? Only: You can still estimate the volume of the earth with some school math, but the density?

Henry Cavendish, an 18th-century British scientist, may have felt the same way.

In fact, thanks to an ingenious experimental setup, he was able to determine the weight of the earth in a very good approximation. The gravitation law discovered by Isaak Newton a century earlier helped him.

So to understand how Cavendish got his results, let's go on an excursus that will take us almost 200 years back.

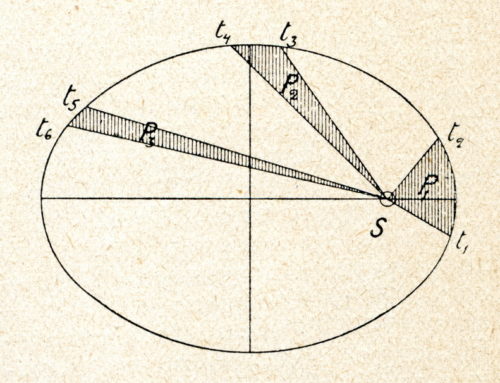
Etwa 1618 hatte Johannes Kepler die nach ihm benannten (siehe auch der Artikel <a title="“Shortcuts" – die keplerschen gesetze“ href="/en/“https://kepler.scinelion.com/shortcuts-die-keplerschen-gesetze/“/" target="“_blank“">hier</a>) Gesetze entdeckt, nach denen sich die Planeten um die Sonne bewegen. Diese fand er rein empirisch, ohne eine Ursache für die mathematisch ästhetischen Zusammenhänge angeben zu können.

Newton was then able to formulate the forces that act between two bodies in his epochal law of gravitation, which on the one hand states that the gravitational force is proportional to the product of the masses of these two bodies, and on the other hand that they become square with increasing distance between the bodies decreases.

This proportionality between force on the one hand and masses or distance on the other is universal (at least there is no reason to assume otherwise), i.e. one can always and everywhere mathematically assume a gravitational constant, the function of which is mathematically only to describe the conversion from the units square meter (distance square) and square kilogram (product of the two masses) to newtons (for the gravitational force).

How did Newton recognize this connection, without the gravitational force between, let's say e.g. to be able to experimentally measure a wooden and a lead ball? Because gravitation is an attraction between any body, even if we mostly consider it in connection with gravity.

The decisive finding on the way to the idea of a gravitational force probably arose from the principle of inertia previously formulated by Galileo Galilei: a body on which no external forces act moves uniformly. Therefore you have to e.g. in the case of planetary movements do not assume any tangentially acting forces that would maintain the speed, but rather directed towards the center, which force the planets onto an ellipse around the sun, i.e. only change their direction.

This leads to a suspicion which, in its consequence, could hardly have been more decisive for the mechanical understanding of the world: it is the sun itself that exerts a force on the planets, just as the earth exerts a force on the moon and vice versa.

The nature and cause of this force remain in the dark, but since Newton no longer its predictability:

The simple formula F = G × (m1 × m2) / r ² , which is derived from Kepler's 3rd law on the one hand and the assumption that gravitation corresponds to a centripetal force directed towards the center of the body, succeeds , Cavendish in turn made it possible to experimentally determine the gravitational constant G.

In doing so, he measured the gravitational force F (see photo) acting between two balls via the elegant detour of the weak twisting of a freely suspended thread, from which he in turn was able to calculate G.

If you now know G again, i.e. the gravitational constant, you can solve the formula according to m ₁ (for the mass of the earth) and the knowledge of the earth's radius (which is, for example, a weight of the earth near it) Distance to earth as mass point equals) determine the mass of the earth.

If the gravitational force acting on a kilogram (according to F = m × g) on Earth is assumed to be 9.81 Newtons, and the gravitational constant determined by Cavendish is approximately 6.7 x 10 ^-11 m ³ / (kg × s ² ), inserting it results in an earth mass of approx. 6 × 10 ²⁴ kg.

Pretty heavy?

What seems so easy mathematically today is the fruit of many errors, ingenious findings and enormous patience and perseverance of many individual minds. So with some awe we stand on the shoulders of giants, amazed at how humans gradually unravel their secrets from the universe through thought.